When we calculate Boolean sums, we have to use several types of Boolean Identities. These are helping to go to the last answer for the given question/sum. Without these we are unable to get the answer. Basically, there are 10 types of boolean identities and they are as following.
01. AND Gate

03. NOT gate
01. Law of double complement
(A' )' = A
02. Idempotent Laws
A + A = A
A . A =A
03. Identity Law
A + 0 =A
A . 1 = A
04. Domination /Null/ Universal bound law
A + 1 = 1
A . 0 = 0
05. Commutative law
A + B = B +A
A . B = B . A
06. Associative Law
A + (B+C) = (A+B) + C
A . (B . C) = (A . B) . C
07. Distributive Law
A . (B + C) = (A . B) + (A . C)
A+ (B . C) = (A + B) . (A + C)
08. De Morgan's Law
(A . B)' = A' + B'
(A + B)' = A' . B'
09. Absorption Law
A . (A + B) = A
A + A .B = A
10. Inverse Law / Unit & zero properties
A + A' = 1
A . A' = 0
*** Remember the laws with their names. As an example sometimes they are asking to prove the De Morgan's Law. So, in this kind of situations it's better to remember the laws with names***
*** Remember the laws with their names. As an example sometimes they are asking to prove the De Morgan's Law. So, in this kind of situations it's better to remember the laws with names***
Logic Gates
In logic gates we are using 2 main numbers. We call it as binary numbers as the base of those numbers is 2. We are using 1 and 0 in binary number system. In other words, 1 is for switch on and the output is as expected. 0 is for switch off and when the switch is off, the output will not be as expected.
Ex: Assume that I have 2 LED bulbs and one bulb is lighted and the other one is darken. In binary, darken one is represented by 0 and the lighted one is represented by 1. That is the basic idea of 1 & 0.
Ex: Assume that I have 2 LED bulbs and one bulb is lighted and the other one is darken. In binary, darken one is represented by 0 and the lighted one is represented by 1. That is the basic idea of 1 & 0.
01. AND Gate

In AND gates the output will be 1(On) when only the both inputs are 1 (Switched on). If one of them are switched off, the output will be 0. These are the attributes of the AND gate.
AND gates are denoted by "." ; For the above example ,
AND gates are denoted by "." ; For the above example ,
A . B = Y
02. OR Gate
OR gates are giving 1 (switched on) output, when at least one input giving 1(switched on). Otherwise it gives 0 as the output. When using 2 input OR gates, it'll get only a one chance to stay in 0(zero) position and in other every possible situation it'll stand as 1(switched on).
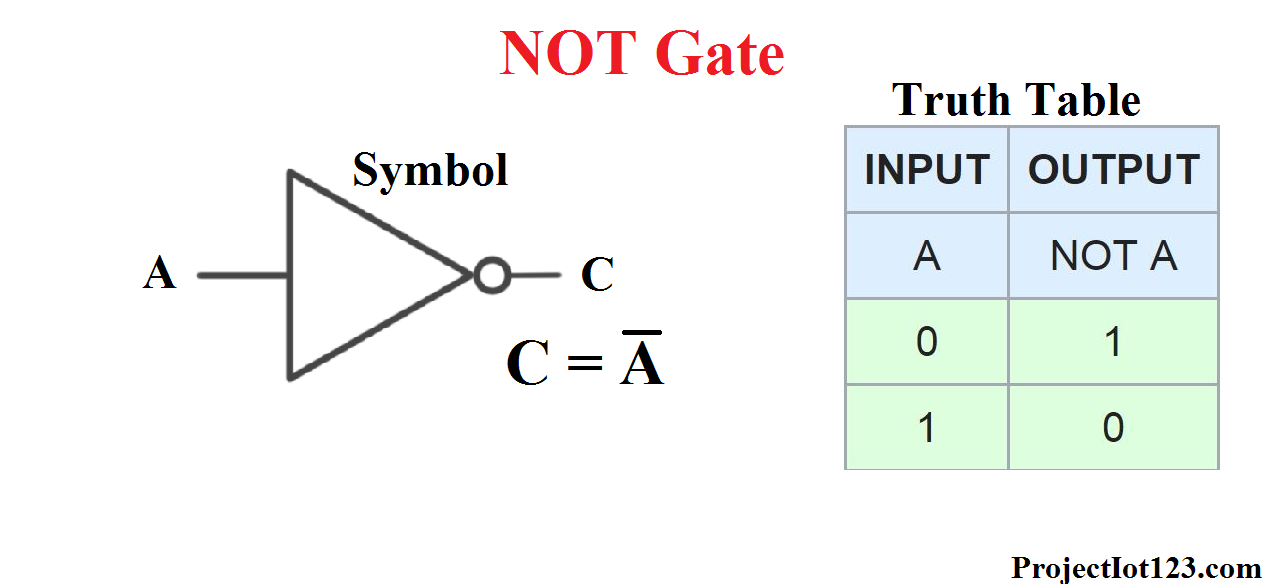
03. NOT gate

NOT gates are represented as above and we can also write above formula as C = A'
I can define NOT gates as a mischievous child. As we all know some little children doesn't obey to their parents and they do the exact opposite thing what they are supposed to do.
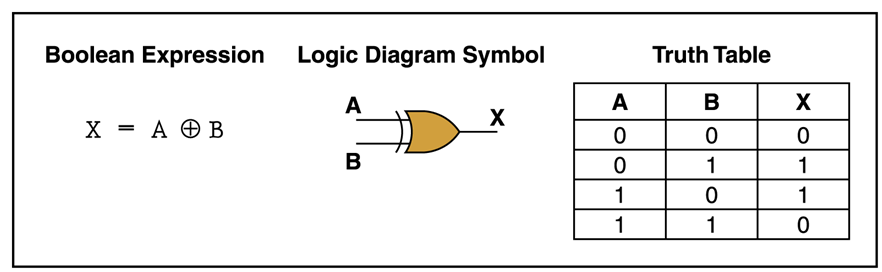
04. XOR gate
XOR gates are as same as the OR gates, but XOR gates give the output as '0' when both of the inputs are '1'.

Comments
Post a Comment